คัดจาก www.matichon.co.th. : บทความพิเศษ โดย ชัยวัฒน์ ถิระพันธุ์
“ความไร้ระเบียบ” ในความหมายทางวิทยาศาสตร์ คือ สภาพและกระบวนการของระบบที่ไร้เสถียรภาพ (unstable) อันมีความอ่อนไหวสูงยิ่งและเปราะบาง เมื่อมีการกระทบเพียงเล็กน้อยในสาเหตุเบื้องต้น (initial condition) แต่เมื่อเกิดบ่อยๆ ซ้ำแล้วซ้ำเล่า เหตุเล็กๆ เพียงเบื้องต้นทำให้เกิดพัฒนาของระบบที่ดำเนินไปอย่างไม่เป็นเส้นตรง เป็นเส้นทางคดเคี้ยว กวัดแกว่ง บางครั้งถึงก้าวกระโดดฉับพลัน ผลลัพธ์ที่เกิดขึ้นจึงทำนายให้ถูกต้องแม่นยำได้ยาก
ทั้งหมดนี้ล้วนแล้วแต่เป็นสิ่งตรงกันข้ามกับแนวคิดหลักที่เชื่อถือกันมาตั้งแต่ศตวรรษที่ 17 ว่า สรรพสิ่งทั้งหลายอยู่ภายใต้กฎเกณฑ์ที่สามารถคำนวณได้อย่างถูกต้องไม่ผิดพลาด ขอให้รู้สมมติฐานอันเป็นเงื่อนไขเบื้องต้นให้ชัดเจน จริงๆ จะสามารถทำนายผลลัพธ์ออกมาได้อย่างแม่นยำ
ตัวอย่างที่เป็นรูปธรรมนั้นเราสามารถศึกษาได้จาก Edward Lorenz แห่งสถาบัน MIT
ตัวอย่างที่เป็นรูปธรรมนั้นเราสามารถศึกษาได้จาก Edward Lorenz แห่งสถาบัน MIT เมื่อกลางทศวรรษที่ 60
อาจารย์ด้านอุตุนิยมวิทยา (meteoro logy) ผู้นี้พยายามสร้างโมเดลการคำนวณในการพยากรณ์อากาศโดยใช้สมการง่ายๆ แสดงการ ปฏิสัมพันธ์ระหว่างอุณหภูมิกับกระแสลม
เขาป้อนข้อมูลที่จุดทศนิยม 6 หลัก คือ 0.506127 เข้าเครื่องคอมพิวเตอร์ซึ่งพิมพ์ผลออกมาทุกๆ นาทีด้วยความ เบื่อที่นั่งคอยผลลัพธ์นานๆ เพราะคอมพิวเตอร์ยุคนั้นทำงานช้า
Lorenz จึงตัดตัวเลขหลังจุดทศนิยมออกไปเสีย 3 หลัก ให้เหลือ 0.506 เขาเอาผลลัพธ์จากระยะหนึ่งมาเป็นจุดเริ่มต้นของการคำนวณ แล้วสตาร์ตโปรแกรมใหม่
ผลของการคำนวณระยะแรกเหมือนกับการทดลองเก่าๆ ที่เคยทำมาครั้งแล้วครั้งเล่า หลังจากลุกไปชงกาแฟแล้ว กลับมาดูตัวเลขใหม่ ปรากฏว่าผลลัพธ์ต่างกันโดยสิ้นเชิง โมเดลของดินฟ้าอากาศไปกันคนละทิศทาง
Lorenz คิดว่าเครื่องคอมพิวเตอร์คงจะมีอะไรผิดพลาด จึงทดลองซ้ำอีก ผลคำนวณยังคงยืนยันว่าความแตกต่างดังครั้งแรก เขาทดลองอีกสองสามครั้ง ซึ่งก็ย้ำความถูกต้องของคอมพิวเตอร์
Lorenz คิดว่าเครื่องคอมพิวเตอร์คงจะมีอะไรผิดพลาด จึงทดลองซ้ำอีก ผลคำนวณยังคงยืนยันว่าความแตกต่างดังครั้งแรก เขาทดลองอีกสองสามครั้ง ซึ่งก็ย้ำความถูกต้องของคอมพิวเตอร์
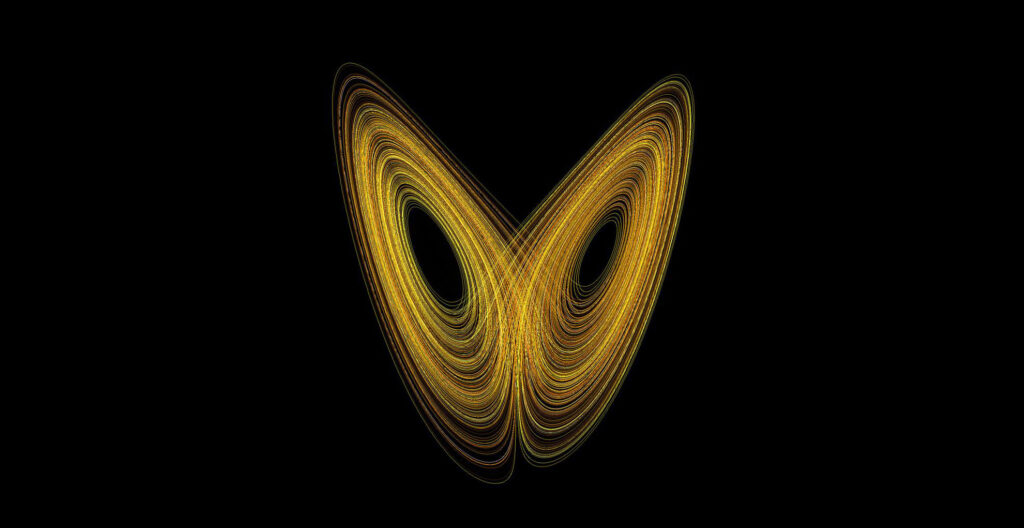
เปรียบเสมือนการไหวตัวของกระแสลมเบาๆ ที่มาจากการกระพือปีกของผีเสื้อแต่กลับกลายไปสร้างผลกระทบใหญ่หลวงทางดินฟ้าอากาศได้ Lorenz จึงขนานนามว่าเป็น “ผลกระทบผีเสื้อ” (butterfly effect) ซึ่งกลายเป็นถ้อยคำที่โด่งดังไปทั่วโลก
ศาสตราจารย์ Lorenz กล่าวว่า “ในทางทฤษฎีด้านอุตุนิยมวิทยา ผีเสื้อใหญ่ตัวหนึ่งกระพือปีกที่ฮ่องกง สามารถทำให้ดินฟ้าอากาศที่แคลิฟอร์เนียเปลี่ยนแปลงเป็นพายุได้เมื่อหนึ่งเดือนให้หลัง”
ทฤษฎีไร้ระเบียบนอกจากพูดถึงความสำคัญของการเปลี่ยนแปลงของสาเหตุเบื้องต้นแล้วยังพูดถึงเรขาคณิตเศษส่วน (fractal geometry) หรือ ไวยากรณ์แห่งทฤษฎีไร้ระเบียบ
มีคนแปลคำว่า geometry ในเชิงภาษาว่า “การวัดแผ่นดิน” และคำว่า fractal มาจากภาษาละติน fractus หรือ fractrum ซึ่งแปลเป็นภาษาอังกฤษว่า fragmented (or irregular) เมื่อแปลเป็นไทย คือ แตกเป็นชิ้น เป็นเศษ
ขณะที่เรขาคณิตคลาสสิกของยูคลิดที่เราเรียนกันเมื่อเป็นเด็ก เป็นเรขาคณิตที่สนใจต่อแบบฟอร์มและรูปร่างในอุดมคติ คือ มีรูปร่างเป็นเส้นตรง วงกลม สามเหลี่ยม สี่เหลี่ยม หรือวงรี รูปร่างและทรงต่างๆ ในเรขาคณิตยูคลิดจึงสะอาด ราบเรียบ สม่ำเสมอ และชัดเจน
แต่เรขาคณิตเศษส่วน หรือ fractal geometry สนใจค้นคว้ารูปทรงที่เป็นจริงของธรรมชาติซึ่งขรุขระ ไม่เรียบร้อย เช่น ใบไม้ ก้อนเมฆ สายฟ้าแลบ ชายฝั่งทะเล ภูเขาและโตรกผา ปอดของมนุษย์ เป็นต้น
มิติของเรขาคณิตเศษส่วนจึงมีลักษณะคล้ายทศนิยมไม่รู้จบ เช่น มิติเศษส่วนของสมองเรา คือ 2, 79 และของก้อนเมฆ คือ 2, 35 มิติเศษส่วนหรือ fractal ในที่นี้จะเป็นสองมิติของพื้นที่ หรือเป็นสามมิติของพื้นที่ หรือเป็นสามมิติแบบทรงลูกเต๋า หรือลูกกลมก็ได้

คุณสมบัติสำคัญของ fractal หรือเศษส่วนไม่รู้จบ คือ “ความคล้ายตนเอง” (self-similarity) นั่นคือ โครงสร้างของเศษส่วนที่ขยายตัวออกไปอย่างไม่สิ้นสุด ไม่ว่าในมิติทางกาล (time) หรือมิติทางเทศะ (space) ล้วนแล้วแต่มีรูปร่างคล้าย คลึงซ้ำกับแบบแผน (pattern) อันแรก อันเป็นแม่แบบของมัน
Benoit Mandelbrot ผู้ค้นคว้าทฤษฎีไร้ระเบียบทางคณิตศาสตร์ สรุปความเชื่อมโยงแนบแน่นระหว่างคณิตศาสตร์เศษส่วนกับทฤษฎีไร้ระเบียบไว้ดังนี้
ความสัมพันธ์ระหว่างรูปร่างที่เป็นเศษส่วน (fractal) กับระบบที่ไร้ระเบียบ (chaotic system) เกิดจากคุณสมบัติข้อที่บอกว่า การเปลี่ยนแปลงที่ขึ้นต่อ (depend) ความอ่อนไหวอย่างยิ่งยวดของเงื่อนไขเบื้องต้น ประกอบกับการพัฒนาลักษณะพลวัตอันซับซ้อนและยอกย้อนกลับไปกลับมา ทำให้เศษส่วนแต่ละอันจึงไม่เหมือนกันร้อยเปอร์เซ็นต์ รูปลักษณ์แต่ละภาพจะมีความคลาดเคลื่อนไปบ้าง เช่น ปุยเมฆแต่ละก้อน ต้นไม้แต่ละต้น ใบไม้แต่ละใบ หัวใจแต่ละดวง และสมองแต่ละก้อน ย่อมต่างกันไปบ้าง
อย่างไรก็ตาม เมื่อเรามองเห็นก็รู้ได้ทันทีว่านี่คือต้นมะม่วง นี่คือต้นมังคุด นี่คือใบโพธิ์ เป็นต้น และนี่เป็นสิ่งที่ทฤษฎีไร้ระเบียบพยายามตอบคำถามว่าทำไมเกล็ดหิมะแต่ละเกล็ดที่โปรยปรายลงมาจึงมีความแตกต่างกันไปเล็กน้อย ก็เนื่องจากว่าผลรวมของตัวแปรที่มีอิทธิพลต่อการเกิดเกล็ดแต่ละเกล็ดต่างกัน
การค้นคว้าในมิติเศษส่วน (fractal) จึงมิใช่การนิยามสัญลักษณ์ทางคณิตศาสตร์ที่ประดิษฐ์ขึ้นมาเอง แต่เป็นการนำเสนอให้เห็นคุณสมบัติอันแท้จริงของสภาพแวดล้อมในระดับต่างๆ ตั้งแต่ขนาดจิ๋ว (micro) จนถึงขนาดยักษ์ (macro) ซึ่งปรากฏอยู่ในโลก
การพัฒนาที่ดำเนินไปในลักษณะเศษส่วนและไร้ระเบียบนั้น น่าสนใจ มิใช่เพียงว่าได้แสดงให้เห็นโครงสร้างที่ไม่สม่ำเสมอ ในระบบพลวัตที่ไม่เป็นเส้นตรงเท่านั้น ความสำคัญอีกข้อหนึ่งซึ่งจะมีประโยชน์ในการสังเกตดูแบบแผนของสรรพสิ่งในโลก (รวมถึงสังคม) คือโครงสร้างไร้ระเบียบ (chaotic structure) เป็นโครงสร้างพื้นฐานของกระบวนการสร้างสรรค์ในธรรมชาติ
ธรรมชาติมีพลังสร้างสรรค์ในการจัดตั้งรูปแบบอย่างมหัศจรรย์ เมื่อได้สร้างแม่แบบเบื้องต้น ขึ้นแล้วรูปแบบอื่นก็จะลอกเลียนตามมา
นักวิจัยไร้ระเบียบเรียกเศษส่วนคล้ายธรรมชาตินี้ว่า “ภาษาของธรรมชาติ” พวกเขาเชื่อว่าวิธีการและรูปแบบที่เรขาคณิตเศษส่วนและทฤษฎีไร้ระเบียบได้ถ่ายทอดความเป็นจริงของโลกออกมานั้น พอจะกล่าวได้ว่าทฤษฎีไร้ระเบียบเป็นเสาหลักของโลกทัศน์ใหม่ได้ และความสำคัญของเศษส่วน (fractal) ในการวิจัยคือ การช่วยทำให้เข้าใจ “จุดดึงดูดไร้ระเบียบ” (chaotic attractors) ได้ดีขึ้น เพราะมันมีโครงสร้างเศษส่วน (fractal structure) อยู่ในนั้น
สรุปอีกครั้งหนึ่งว่า เมื่อระบบพลวัตเคลื่อนตัวเข้าสู่สภาพไร้ระเบียบ รูปแบบและโครง สร้างของความไร้ระเบียบสามารถใช้เรขา คณิตเศษส่วนอธิบายให้เข้าใจ
และในทางกลับกัน ทฤษฎีไร้ระเบียบช่วยในการคิดค้นว่า โมเดลอะไร กลไกอะไร ที่มีส่วนทำให้เกิดโครงสร้างเศษส่วนขึ้นมา การค้นพบดังกล่าวทำให้เกิดประโยคที่ว่า การวิจัยความไร้ระเบียบคือรากฐานของศาสตร์แขนงใหม่
เป็น “ศาสตร์อนิจจัง” (science of becoming)

